Fizyczne podstawy dźwięku i tercjowej budowy akordów
Czym jest dźwięk?
Podstawą muzyki i nauk z nią związanych są dźwięki. Wiele zagadnień muzycznych nie może być omawianych bez zrozumienia istoty dźwięku. Wspomnijmy chociażby o melodii, czyli wielu dźwiękach następujących jeden po drugim, o akordach, które są w rzeczywistości strukturami powstałymi z połączenia przynajmniej trzech dźwięków różnej nazwy i wysokości1.
Generalnie rzecz biorąc, dźwięk jest zjawiskiem fizycznym (akustycznym), powstającym na skutek drgań ciał sprężystych, wprawiających w drgania powietrze docierające do narządów słuchu. Ciała sprężyste to pojęcie z dziedziny fizyki. Muzycznie rzecz ujmując, ciało sprężyste to któryś z elementów instrumentu. I tak, dla fortepianu będą to napięte struny, które zostają wprawiane w drgania po uderzeniu w nie mechanizmem połączonym z klawiszami. Dla gitary będą to uderzone ręką lub piórkiem struny. W harmonijce ustnej będą to blaszki wprawione w drgania po zadęciu w otwory. W większości przypadków drga struna (gitara, harfa), słup powietrza po zadęciu (instrumenty dęte), metalowy lub drewniany element (ksylofon).
Rodzaje dźwięków
Badając właściwości dźwięków można wyróżnić dwa typy: regularne i nieregularne. W muzyce zdecydowanie większe znaczenie mają dźwięki regularne, to jest takie, w których ilość drgań jest jednakowa w różnych odstępach czasu. Powoduje to, że dźwięk ma pewną określoną wysokość. Najprostszym z możliwych przypadków dźwięku regularnego jest ton prosty, który przyjmuje kształt sinusoidy. Sinusoidę2 można zdefinować podając jej częstotliwość (lub okres, który jest odwrotnością częstotliwości) i amplitudę. Częstotliwość ma wpływ na wysokość dźwięku, amplituda to moc, głośność dźwięku. Tony proste nie mają wielkiego znaczenia w muzyce, bo dźwięk takiej prostej fali jest dla ucha nieprzyjemny3. Dzwięki nieregularne można odnaleźć w instrumentach perkusyjnych, ale nie są one tak atrakcyjnym obiektem badań jak dźwięki regularne. Nie da się na nich zagrać melodii, nie da się ich połączyć w akordy (choć oczywiście można mówić o pewnym współbrzmieniu tych instrumentów.
Każdy dźwięk wydawany przez instrument muzyczny jest sumą pewnej ilości tonów prostych, co sprawia, że nazywamy go dźwiękiem regularnym złożonym. Niektóre syntezatory posługują się czasem techniką zwaną syntezą addytywną, która polega na sumowaniu tonów prostych, w wyniku czego otrzymujemy dźwięki do złudzenia przypominające żywe instrumenty. Zwykle syntezę addytywną zatrzymuje się na pewnym etapie dodając skończoną liczbę sinusoid. W rzeczywistości ilość tonów i ich częstotliwości dążą do nieskończoności, ale na pewnym etapie ucho nie jest już w stanie wychwycić różnic (lub po prostu ogranicza się wymagania sprzętowe lub programowe syntezatorów). Dość podobną, i nawet częściej stosowaną techniką jest synteza subtraktywna, w której zamiast sumować tony proste, odejmuje się je.
Dźwięk muzyczny przyjmuje swoją nazwę od tonu najniższego, który jest jednocześnie tonem najsilniej brzmiącym. Taki ton nazywamy tonem podstawowym. Tony pozostałe, każdy kolejny coraz wyższy i jednocześnie coraz słabszy, noszą w fizyce i muzyce nazwę tonów harmonicznych. Zwane są one również tonami górnymi, przytonami lub z łaciny alikwotami. Można się także spotkać z pojęciem flażoletów, ale słowo flażolety jest częsciej używane w kontekście sposobu wydobywania kolejnych składowych harmonicznych4.
Skąd się bierze skala naturalna?
Cała ta teoria sprowadza nas do najbardziej istotnych aspektów podstaw budowy dźwięku. Otóż szereg tonów harmonicznych należących do dowolnego tonu podstawowego tworzy z nim tzw. skalę naturalną. Co więcej, okazuje się, że tony harmoniczne pozostają z tonem podstawowym w stałym stosunku. Ten stosunek wynosi dla kolejnych harmonicznych 2, 3, 4, 5, 6 i tak dalej.
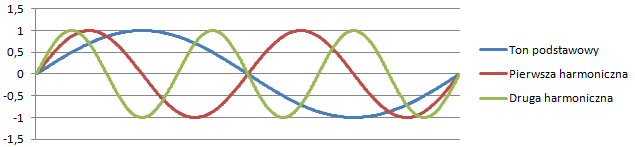 Rys. 1. Wykres trzech pierwszych tonów dowolnego dźwięku o długości odpowiadającej fali pierwszego tonu. Warto zwrócić uwagę na charakterystyczne punkty wspólne na początku, w środku i na końcu wykresu.
Rys. 1. Wykres trzech pierwszych tonów dowolnego dźwięku o długości odpowiadającej fali pierwszego tonu. Warto zwrócić uwagę na charakterystyczne punkty wspólne na początku, w środku i na końcu wykresu.
Jest to konsekwencją tego, że poza drganiem struny jako całości, samoczynnie powstają w niej węzły dzielące całość na dwa, trzy itd. elementy. Każda połówka struny drga tonem dwa razy mniejszym, każda trzecia częśc drga tonem trzy razy mniejszym, i tak teoretycznie do nieskończoności. Teoretycznie, po w pewnym momencie tony są tak złabe, że przestają być słyszalne. Najmocniejszy ton podstawowy bierze się z tego, że struna drga jako całość, pierwsza harmoniczna powstaje na skutek drgania każdej z połówek całej struny, Trzeci ton (czyli druga harmoniczna) powstaje dlatego, że niezależnie od reszty struna drga w trzech róznych kawałkach.
Do ciekawych wniosków można dojść analizując kolejne częstotliwości dźwięku A (220 Hz):
220 Hz (ton podstawowy)440 Hz (pierwsza harmoniczna, dźwięk o oktawę wyższy, dźwięk A)
660 Hz (druga harmoniczna, dźwięk o duodecymę wyższy, dźwięk E)
880 Hz (trzecia harmoniczna, dźwięk wyższy o dwie oktawy, dźwięk A)
1100 Hz (czwarta harmoniczna, dźwięk wyższy o 28 półtonów, dźwięk Cis/Des)
1320 Hz (piąta harmoniczna, dźwięk wyższy o 31 półtonów, dźwięk E)
1540 Hz (szósta harmoniczna, dźwięk wyższy o 34 półtony, dźwięk G)
Tu małe sprostowanie: częstotliwości nie pokrywają się idealnie i matematyk miałby do tego pewne zastrzeżenia. 660 Hz to nie jest dokładnie dźwięk E. E duodecymę wyższe to 659,26 Hz. Częstotliwość jest minimalnie zawyżona. Podobne róznice występują w Cis/Des, ale w tym przypadku częstotliwość jest zaniżona. Kolejne E ma częstotliwość właściwą w prybliżeniu równą 1318,51 Hz, a nie wskazane 1320 Hz (znów zawyżone). Przy kolejnym G znów jest zaniżone. Analizę kolejnych harmonicznech pozostawiam dociekliwym czytelnikom.
Co wynika z tych rozważań?
Zastanówmy się z czego składa się akord A. Ano z dźwieków A Cis i E, czyli z tonu podstawowego, czwartej harmonicznej oraz drugiej harmonicznej. Pięć tonów prostych tworzy nam akord durowy. Pójdźmy dalej i pomyślmy z czego składa się akord A7. Ano z dźwięków A Cis E G, czyli z tonu podstawowego, czwartej harmonicznej, drugiej (piątej) harmonicznej i szóstej harmonicznej. Siedem tonów prostych tworzy nam akord septymowy. A co z akordem A9? Szósta harmoniczna to 1540 Hz, siódma to 1540+220=1760 [Hz], ósma to 1760+220=1980 [Hz]. 1975,53 Hz to dźwięk H, czyli piąty dźwięk z pięciodźwięku A9. A9 to dźwięki A, Cis, E, G, H. Wniosek: dziewięć półtonów wystarczy do utworzenia akordu nonowego. Dalszą analizę pozostawiam czytelnikom. Warto wspomnieć w tym miejscu o tzw. riffach, które są dość mocno eksploatowane w muzyce rockowej. Są to dwudźwięki składające się z prymy i kwinty. Riff A (oznaczany też jako A5) to dźwięki A i E. Do takich zagrywek wystarczą trzy kolejne tony. Częstotliwości prymy i kwinty dość ładnie się pokrywają (częstotliwości prymy i kwinty w jednej oktawie są w stosunku 2/3), co jest szczególnie istotne w przypadku mocno przesterowanych gitar. Mocno przesterowane czterodźwięki, pięciodźwięki brzmią, nie bójmy się użyć tego słowa, źle.
Aby sprawdzić i przekonać się, że rzeczywiście w drgającej strunie powstają samoczynnie węzły fali, a w konsekwencji kolejne harmoniczne można wykonać eksperyment. Weźmy gitarę nastrojoną tradycyjnie, czyli licząc od najgrubszej struny do dźwięków E, A, D, G, H i E. Uderzmy basową strunę E i wsłuchajmy się w wyższe częstotliwości. Powinniśmy usłyszeć dźwięk pustej struny H, nieco wyższy dźwięk Gis (czwarty próg najcieńszej struny). Dalsze składowe są mniej słyszalne (co nie oznacza, że nie da się ich usłyszeć).
Warto jeszcze na koniec zaznaczyć, że wspomniane fizyczne właściwości drgań doprowadziły do czegoś takiego jak tercjowa budowa akordów. Odrzucając powtarzające się tony (ton podstawowy, pierwsza i trzecia harmoniczna to dźwięk A, druga i piąta harmoniczna to dźwięk E) i układając je od najniższego dźwięku do najwyższego okaże się, że tworzą nam się kolejne tercje. Stąd właśnie tercjowa budowa akordów. Jak już zostało napisane, powstają nam kolejno akordy A, A7, A9, a potem także A11, A13.
1Współbrzmienie kilku dźwięków różnej wysokości, ale tej samej nazwy nie jest akordem. Współbrzmienie zatem trzech dźwięków A pochodzących z różnych oktaw nie jest akordem, a jedynie wzmocnieniem dźwięku A o najniższej częstotliwości. Dźwięk A o częstotliwości 220 Hz w sposób naturalny dzieli falę tworząc dźwięki A o częstotliwościach 440 Hz i 880 Hz (i kolejne). Zagranie zatem dźwięków A przesuniętych wielokrotność oktawy tylko wzmocni podstawowy dźwięk. Dźwięki przy prawidłowo wykonanym i nastrojonym instrumenci powinny się zlać.
2Podobne parametry ma cosinusoida. Do analizy nadaje się ona tak samo jak sinusoida. Obie funkcje matematyczne różnią się przesunięciem fazowym. Cosinus jest opóźniony w stosunku do sinusa o 1/4 okresu. Przesuwając cosinusa o 1/4 okresu do przodu sprawimy, że obie funkcje o tym samym okresie i amplitudzie dokładnie się pokryją.
3Większość naturalnych dźwięków ma bardziej złożony charakter i do takich złożonych dźwięków ucho jest bardziej przyzwyczajone. Ton prosty wydaję się piskliwy i jest nieprzyjemny w odbiorze.
4Sposób wydobywania flażoletów/alikwotów opiera swoje działanie na technice tłumienia tonu podstawowego. W instrumentach strunowych możemy lekko przyłożyć palec na środku struny tłumiąc w ten sposób podstawową harmoniczną, sprawiając jednocześnie, że najmocniej brzmieć będzie pierwsza harmoniczna (pierwsza harmoniczna ma dwa razy większą częstotliwość. Fala podstawowego tonu ma długość całego elementu czynnego struny, fala pierwszej harmonicznej jest podzielona w połowie. Palec przyłożony w połowie struny nie tłumi więc drugiej składowej dźwięku w takim samym stopniu jak pierwszej.
widac wlozone serce, duzo pracy, ciesze sie widzac wklad w to aby caly swiat spiewal i gral.

Szukaj z google:
Na skróty:
 | Przetransponuj akordy do dowolnej tonacji: Transponowanie akordów |
 | Znajdź nazwę akordu na podstawie dźwięków składowych: Wyszukiwanie akordów |
 | Wygeneruj dźwięk/akord midi na podstawie wybranych klawiszy fortepianu: Generowanie dźwięków/akordów MIDI |
 | Zbadaj swój słuch w zakresie rozpoznawania różnic częstotliwości lub sprawdź zdolność słyszenia wysokich częstotliwości. |
 | Pytania, zgłoszenia związane z prawami autorskimi (blokowanie i udostępnianie pełnych tektów): Formularz kontaktowy |
 | Zobacz zespoły naszych użytkowników lub dodaj swój: Zespoły naszych użytkowników |
 | Zobacz piosenki oczekujące na akceptację: Poczekalnia |
 | Zapoznaj się z polityką prywatności na stronie: Polityka prywatności |
Reklama:
Aby umieścić reklamę na stronie CDur.pl skontaktuj się z redakcją korzystając z formularza
Cdur.pl dąży do popularyzacji zamieszczonych utworów i ułatwienia edukacji muzycznej. Zamieszczone opracowania akordów mają pomóc w grze na gitarze, fortepianie, pianinie i innych instrumentach. Szanujemy pracę twórców zamieszczonych dzieł. Jeżeli umieszczenie tekstu utworu jest sprzeczne z czyimiś prawnymi lub osobistymi interesami, uprzejmie prosimy o kontakt przy pomocy poczty elektronicznej cdurinfo@gmail.com.
